AP Physics B and C- Equations to be Remembered in Circular Motion and Rotation

In the section ‘Circular motion and rotation’, the sub sections included as common for AP Physics B and C are

(1) Uniform circular motion and

(2) Torque and rotational statics.

The sub sections included for AP Physics C only are

(1) Rotational kinematics and dynamics and

(2) Angular momentum and its conservation.

Circular motion and rotation’ carries 4% of the total points for AP Physics B and 9% of the total points for AP Physics C.

Here are the important equations you need to remember to tackle the AP Physics B Examination:

(1) When an object is in uniform circular motion, the magnitude of its centripetal acceleration (a_c) is given by

a_c = v²/R where ‘v’ is the speed of the object and R is the radius of the circle. The direction of a_c is always towards the centre of the circle.

The angular speed ω is related to the speed v by

v = ωR.

Therefore, the centripetal acceleration is a_c = ω²R.

If T is the time period of revolution of the object in circular motion and f is its frequency, we have f = 1/T and ω= 2π/T = 2πf.

The centripetal force required to produce circular motion is mv²/R = mω²R

(2) Angular acceleration (α) is the time rate of change of angular velocity and is given by

α = dω/dt

In the case of a body in accelerated rotational motion, the angular velocity (ω) after a time t is given by

ω = ω₀ + αt where ω₀ is the initial angular velocity and and α is the angular acceleration. [This is similar to the equation, v = v₀ + at in linear motion].

The angular displacement (θ) at the instant t is given by

θ = θ₀ + ω₀t + (½) αt² where θ₀ is the initial displacement (at t =0)

[This is similar to the equation x = x₀ + v₀t + (½) at² in linear motion].

(3) Torque (τ) is the moment of force and is the product of force and the lever arm. By lever arm we mean the perpendicular distance (ON in the figure) of the line of action of the force from the origin.

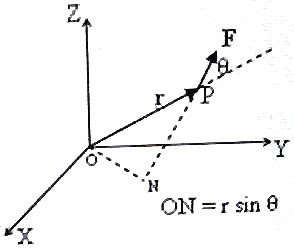
Therefore, Torque τ produced by the force F acting on the particle at P = ON × F.

Since ON = r sinθ where θ is the angle between r and F,

τ = rF sinθ

[Note that torque (τ) is a vector which is the vector product of the position vector r and the force vector F. Therefore, torque τ = r × F]

(4) A rigid body will be in mechanical equilibrium, if the total force and the total torque on the body are zero. The condition of zero net force will ensure that there is no change in the linear momentum and the condition of zero net torque will ensure that there is no change in the angular momentum.

For AP Physics C Examination, you will require the following also (in addition to the above):

(5) Consider a particle of mass m and linear momentum p. If the position vector of the particle is r, the angular momentum L of the particle with respect to the origin is given by

L = r × p

L is a vector whose magnitude is rpsinθ where r is the distance of the particle from the origin, p is the magnitude of the linear momentum vector p and θ is the angle between the vectors r and p.

Angular momentum is the moment of the linear momentum and is the product of linear momentum and the lever arm r sinθ. [By lever arm we mean the perpendicular distance of the line of action of the linear momentum from the origin].

(6) Moment of inertia (I)of a system of particles (as in the case of a rigid body) about an axis (of rotation) is given by

I = ∑mr² where m is the mass of a particle at perpendicular distance r from the axis of rotation and the summation is for all the particles.

Radius of gyration (k) is related to moment of inertia (I) and the mass of the body (M) as

I = Mk²

Note that both I and k depend on the axis of rotation.

Parallel axes theorem states that the moment of inertia (I)of a body about any axis is equal to the sum of the moment of inertia (I_CM )of the body about a parallel axis through its centre of mass and the product Ma² where M is the mass of the body and a is the distance between the two axes:

I = I_CM + Ma²

Perprndicular axes theorem states that the moment of inertia of a lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.

[For example, if the X and Y axes are in the plane of the lamina, the Z-axis is the perpendicular axis and we have I_Z = I_X + I_Y where I_Z, I_X and I_Y are the moments of inertia about the Z, X and Y-axes respectively]

Moments of inertia of some regular bodies are given below:

(i) Thin circular ring (Mass M, Radius R) about its central axis perpendicular to its plane: MR²

A hollow cylinder (pipe) also has the above value for its moment of inertia about its own axis.

(ii) Thin circular ring (Mass M, Radius R) about any diameter: MR²/2

(iii) Thin rod (Mass M, Length L) about a perpendicular axis through the mid point: ML²/12

(iv) Circular disc (Mass M, Radius R) about its central axis perpendicular to its plane: MR²/2

(v) Circular disc (Mass M, Radius R) about its diameter: MR²/4

(vi) Solid cylinder (Mass M, Radius R) about the axis of the cylinder: MR²/2

(vii) Solid sphere (Mass M, Radius R) about its diameter: (2/5)MR²

(viii) Hollow sphere (Mass M, Radius R) about its diameter: (2/3)MR²

(7) Angular momentum (L) is given by

L = Iω where I is the moment of inertial about the axis of rotation and ω is the angular velocity.

This is similar to the expression for linear momentum p = mv. In angular motion (rotational motion) I is to be used in place of m and ω is to be used in place of v.

Newton’s 2^nd law in rotational motion is

τ = dL/dt = d(Iω)/dt

If the moment of inertia (I) is constant, as is the case of a rigid body rotating about a fixed axis, we can write

τ = I (dω/dt) = I α where α is the angular acceleration.

The law of conservation of angular momentum states that in the absence of external torque, the angular momentum of a system remains unchanged. This can be expressed as

I₁ ω₁ = I₂ ω₂ where I₁ and I₂ are the initial and final moments of inertia and ω₁ and ω₂ are the initial and final angular velocities of a system in the absence of external torques.

(8) Acceleration (a) of a body rolling down an inclined plane of inclination θ is given by

a = gsinθ / [1 + (k²/R²)] where R is the radius of the body and k is the radius of gyration about the axis of rolling.

Since Mk² = (2/5)MR² for a solid sphere, k²/R² = 2/5. This is the least value in the case of regular bodies and hence the acceleration a is maximum in the case of a solid sphere. In contrast, in the case of a ring (and pipe), the value of k²/R² is 1 and is the maximum in the case of regular bodies and hence the acceleration a is the minimum in the case of a ring.

If differently shaped bodies are allowed to roll down from the top of an inclined plane, the solid sphere will reach the bottom first and the ring (and the pipe) will arrive last. It is interesting to note that for a given shape, the time of arrival at the bottom is independent of mas and size.

The above equation for acceleration down the plane can also be written as

a = (Mgsinθ) / [M + (I/R²)] where M is the mass of the body; but it will be better to remember the above form in terms of the radius of gyration, k.

(9) Rotational kinetic energy (K) of a body is given by

K = (½) Iω²

(10) A rolling body has translational and rotational kinetic energies. The total kinetic energy of a rolling body is therefore given by

K = (½) Mv² + (½) Iω² where v is the linear velocity of the body

(11) Work (dW) done by a torque τ in producing an angular displacement dθ is given by

dW = τ dθ [By dW we mean the small amount of work done for a small angular displacement dθ]

This is similar to the expression for work, dW = Fds in linear motion.

(12) Power (P) in rotational motion is given by

P = τω

This is similar to the expression for power, P = Fv in linear motion

Different quantities in linear motion and the corresponding quantities in rotational motion (about a fixed axis) are given below:

(a) Displacement x → Angular displacement θ

(b) Velocity v = dx/dt or dr/dt→ Angular velocity ω = dθ/dt

(c) Acceleration a = dv/dt → Angular acceleration α = dω/dt

(d) Mass M→ Moment of inertia I

(e) Linear momentum p = Mv→ Angular momentum L = Iω

(f) Force F = Ma →Torque τ = I α

(g) Work dW = Fds → Work dW = τ dθ

(h) Kinetic energy K = Mv²/2→ Kinetic energy K = Iω²/2

(i) Power P = F v→ Power P = τω

In the next post, we will discus typical questions in this section.