AP Physics C– Multiple Choice Questions on Circular Motion and Rotation

In the post dated 24^th January 2008, we had discussed some multiple choice questions (on circular motion and rotation) of common interest to AP Physics B as well as AP Physics C aspirants.

As promised in that post, I give below some typical questions in this section, for the benefit of those preparing for the AP Physics C examination:

(1) A wheel starts from rest and rotates through 1000 radians in 10 s under the action of a constant torque. If the moment of inertia of the wheel is 4 kg m², the torque acting on the wheel is

(a) 10 Nm

(b) 20 Nm

(c) 40 Nm

(d) 80 Nm

(e) 100 Nm

The angular displacement (θ) at the instant t is given by

θ = θ₀ + ω₀t + (½) αt² where θ₀ is the initial displacement (at t =0), ω₀ is the initial angular velocity and α is the angular acceleration.

Substituting the known values in the above equation, we have

1000 = 0 + 0 + (½) α × 10², so that α = 20 radian per second².

Torque, τ = I α = 4×20 = 80 Nm

(2) A small solid cylinder rolls up along a curved surface (fig.) with an initial velocity v. It will ascend up to a height ‘h’ equal to

(a) 3v²/2g

(b) 3v²/4g

(c) v²/2g

(d) v²/4g

(e)3v²/g

Since the cylinder is rolling, it has translational and rotational kinetic energies. The total kinetic energy is K = (½) Mv² + (½) Iω² where M is the mass, I is the moment of inertia and ω is the angular velocity of the cylinder. At the highest point, the kinetic energy will be zero since the entire energy will be converted into gravitational potential energy Mgh where h is the height. So. we have

(½) Mv² + (½) Iω² = Mgh

The moment of inertia of the cylinder about its own axis is I = (½) MR² where R is the radius of the cylinder. The angular velocity ω = v/R. Substituting these in the above equation,

(½) Mv² + (½)×(½) MR² ×v²/R² = Mgh

Or, (¾)Mv² = Mgh, from which h = 3v²/4g

Now, suppose we change the above question as follows:

A small cylinder rolling with a velocity v along a horizontal surface encounters a smooth inclined surface. The height ‘h’ up to which the cylinder will ascend is

(a) 3v²/2g

(b) 3v²/4g

(c) v²/2g

(d) v²/4g

(e)3v²/g

You should remember that a body can roll along a surface only if the surface is rough (so that there is frictional force). On a smooth surface the body can slide; but it cannot have a linear displacement by rolling. [You might have seen how a car tyre rotates in mud without producing any movement of the car].

In the present problem, the body will roll up to the foot of the inclined smooth surface. It will continue to spin with the angular speed it has acquired, and will slide up to a certain height, maintaining its spin motion throughout the smooth surface. Its translational kinetic energy alone is responsible for its upward motion along the smooth incline so that the height up to which it will rise is given by

(½) Mv² = Mgh

Therefore, h = v²/2g.

(3) Two inclined planes have same height but different lengths (and therefore different angles). If a solid sphere is allowed to roll down from the top of these inclined planes

(a) the time of descent will be same, but the speed at the bottom of the plane will be greater for the longer plane

(b) the time of descent will be same, but the speed at the bottom of the plane will be smaller for the longer plane

(c) the time of descent and the speed at the bottom will be same in both cases

(d) time of descent will be different, but the speed at the bottom will be same in both cases

(e) speeds and the times of descent will be different

A body rolling down an inclined plane has greater acceleration if the angle (θ) of the plane is greater.

[The expression for the acceleration is a = gsinθ / [1 + (k²/R²)], as given in he post dated 20^th January 2008, but you can solve this problem even without remembering this equation]

The length of the steeper inclined plane is smaller since the planes have the same height. Because of the larger value of θ and the smaller distance to be traveled, the time taken in the case of the shorter plane is smaller.

The velocity of the sphere at the bottom of the plane is determined by the height of the plane since the kinetic energy at the bottom is equal to the gravitational potential energy at the top, as we have seen in the previous question.

[In the case of a sphere, the equation will be (½) Mv² + (½)×(²/₅)) MR² ×v²/R² = Mgh, since the moment of inertia is (²/₅)) MR²].

Since the height is the same, the speed at the bottom will be the same. Therefore, the correct option is (d).

(4) A metre stick AB hinged (without friction) at the end A as shown in the figure is kept horizontal by means of a string tied to the end B, the other end of the string being tied to a hook. The string is carefully cut (or burnt), and the scale executes angular oscillations about an axis passing through the end A. What is the speed of the end B when the metre stick assumes vertical position immediately after the string is burnt? (Acceleration due to gravity = 10 ms^–2)

(a) 2.5 ms^–1

(b) 4.2 ms^–1

(c) 5.4 ms^–1

(d) 6.8 ms^–1

(e) 9.8ms^–1

The centre of gravity of the metre stick is at its middle. When the string is burnt, the height of the centre of gravity is reduced by 0.5 m, thereby reducing the gravitational potential energy of the metre stick by Mgh = M×10×0.5 = 5M joule, where M is the mass of the metre stick.

The decrease in the potential energy is equal to the increase in kinetic energy. Therefore in the vertical position of the metre stick, its kinetic energy

(½)Iω² = 5M

Since the moment of inertia of a uniform bar of length L about a normal axis through ite mid point is ML²/12, its moment of inertia about a parallel axis through its end is ML²/3. [You will get this by applying the parallel axis theorem (see the post dated 2o^th January 2008)]

Therefore, we have (½)(ML²/3)ω² = 5M

Since ω = v/L and L = 1 metre, the above equation becomes

v²/6 = 5, from which v = √30 = 5.4 ms^–1 (approximately).

You will find some useful posts in this section at http://www.physicsplus.in

AP Physics B and C– Multiple Choice Questions on Circular Motion and Rotation

The following questions will be of common interest to AP Physics B as well as AP Physics C aspirants:

(1) A fighter pilot flies along a vertical circle of radius 1 km. At the topmost point of the circle, he feels weightless. What is the speed of the fighter plane? (Acceleration due to gravity = 10 ms^–2)

(a) 25 ms^–1

(b) 50 ms^–1

(c) 75 ms^–1

(d) 100 ms^–1

(e) 125 ms^–1

He feels weightless since his weight is balanced by the centrifugal force so that we have

mv²/R = mg where m is the mass of the plane (with the pilot), R is the radius of the circle and v is the speed of the plane at the topmost point.

Therefore, v = √(Rg) = √(1000×10) = 100 ms^–1.

(2) A door can be opened by pushing with a force of at least 50 N at a point distant 80 cm from the line of the hinges. The minimum force required to open the door by pushing at another point distant 20 cm from the line of the hinges is

(a) 200 N

(b) 100 N

(c) 50 N

(d) 25 N

(e) 12.5 N

The minimum torque (moment of force) required to open the door is given by

τ = r × F

The magnitude of the torque is τ = rF sin 90º, since the force is to be applied perpendicular to the plane of the door to produce maximum torque (so that the applied force is minimum).

Since the minimum torque required is the same in both cases, we have

0.8×50 = 0.2×F where F is the force required to open the door by pushing at a point distant 20 cm from the line of the hinges.

This gives F = 200 N.

(3) A wheel of radius R is rolling along a horizontal surface with a speed u. A pebble trapped on the wheel gets separated from the highest point of the wheel when the wheel arrives at position P (fig.). The horizontal range PQ of the pebble is

(a) u√(R/g)

(b) 2u√(R/g)

(c) 4u√(R/g)

(d) u²√(R/g)

(e) 2u²√(R/g)

Considering the vertical motion of the projectile (pebble), the time taken to reach the ground after leaving the wheel is given by

2R = 0 + (½)gt², from which t = 2√(R/g)

[We have used the equation of one dimensional motion, x = x₀ + v₀t + (½) at²]

The horizontal range of the pebble is PQ = horizontal velocity×time of flight

The centre of mass of the wheel is moving with speed u. The pebble at the topmost point of the wheel is moving horizontally with speed u with respect to the wheel so that the horizontal velocity of the pebble with respect to the ground is u+u = 2u.

Therefore, horizontal range PQ = 2u ×2√(R/g) = 4u√(R/g)

In the next post we will discuss questions in this section solely for the benefit of AP Physics C aspirants.

Example isn't another way to teach, it is the only way to teach.

– Albert Einstein

AP Physics B and C– Answer to Free-response Question on Circular Motion

In the post dated 22^nd January 2008, the following free-response question for practice was given to you:

A simple pendulum of length ℓ is suspended from the point O (fig.). The bob of the pendulum is a sphere of mass m and is initially at rest at A. An identical sphere S (not shown in the figure), which is a projectile with its trajectory in the plane of the figure, has its highest point at A. The projectile therefore collides (elastically) with the bob of the pendulum at A and makes it move with horizontal speed V₁ as shown. The acceleration due to gravity at the place is g.

(a) If the speed V₁ of the bob of the pendulum is just sufficient to make it travel along the circular path of radius ℓ, derive an expression for the speed V₂ of the bob at the highest point B of the circular path.

(b) Derive an expression for the kinetic energy of the bob in terms of m, ℓ and g just when it starts moving from A.

(c) Obtain an expression for the speed of the bob at C, when the string of the pendulum is horizontal.

(d) What was the kinetic energy of the projectile (sphere S) just before it collided with the bob? Give reason for your answer without writing theoretical steps.

(e) Briefly explain the nature of the motion of the projectile after hitting the bob.

As promised, I give below the answer:

(a) Since the bob just moves along the circular path, the centripetal force required for the circular motion at the highest point B is supplied by the weight mg alone. The tension in the string will be zero in this case so that we have, at B,

mV₂²/ℓ = mg

Therefore, V₂ = √(ℓg).

(b) The bob has gained gravitational potential energy mgh = mg×2ℓ = 2mℓg, on moving up from A to B, by losing an equal amount of kinetic energy. The kinetic energy of the bob at B is (½) mV₂² = (½) mℓg, since V₂ = √(ℓg).

Therefore, the kinetic energy (K_A ) of the bob at the lowest point A must be given by

K_A = 2mℓg +(½) mℓg = (5/2) mℓg

(c) The bob has gained gravitational potential energy mgℓ on moving up from A to C (through a height ℓ), by losing an equal amount of kinetic energy. The kinetic energy (K_C) of the bob at C is therefore gien by

K_C = (5/2) mℓg – mℓg = (3/2) mℓg

The speed V₃ of the bob at C is therefore given by

(½) mV₃² = (3/2) mℓg, from which V₃ = √(3ℓg)

(d) When a moving sphere suffers a head-on elastic collision with an identical stationary sphere, the entire kinetic energy of the moving sphere is transferred to the stationary sphere. (The velocities get interchanged).

The kinetic energy of the projectile (sphere S) just before hitting the bob was therefore equal to the kinetic energy of the bob just after the hit: (5/2) mℓg

(e) The projectile will momentarily come to rest on hitting the bob and will fall freely under gravity (vertically) thereafter.

Here are some additional points you must note in the present context:

Suppose in the above question, you were asked to find the tension T₃ in the string when the bob is in position C. You will then answer like this:

Since the string is horizontal when the bob is at C, the centripetal force required for the circular motion of the bob is supplied solely by the tension T₃ in the string and so we have

mV₃²/ℓ = T₃

Since V₃ = √(3ℓg) we obtain T₃ = 3mg.

If you are asked to find the tension T₁ in the string when the bob is in its lowest position A, you will answer like this:

In position A of the bob, the centripetal force is supplied by the resultant of two forces: (i) Tension T₁ which tries to pull the bob vertically upwards

(ii) Weight mg of the bob which acts vertically downwards

Therefore, we have mV₁²/ℓ = T₁ – mg so that

T₁ = mV₁²/ℓ + mg

Since the kinetic energy (½) mV₁² of the bob at A is (5/2) mℓg, we have

V₁ = √(5ℓg)

Substituting this value of V₁ in the above expression for T₁, we obtain

T₁ = 6mg

If the bob is just able to move along the vertical circle, the tension T₂ in the string when the bob is at the top (position B) of the circle is zero and hence the difference between the tensions is

T₁ – T₂ = 6mg

You can easily show that this difference is 6mg in the case of any vertical circle [even if V₁ is greater than √(5ℓg)].

You should remember that the minimum velocity required for the bob at the lowest point A so as to make the bob move along the circular path is √(5ℓg) = √(5Rg), using symbol R for the radius of the circle.

You will often find questions making use of this fact.

AP Physics B and C- Free-response Question on Circular Motion

Here is a question involving circular motion, for your practice:

A simple pendulum of length ℓ is suspended from the point O (fig.). The bob of the pendulum is a sphere of mass m and is initially at rest at A. An identical sphere S (not shown in the figure), which is a projectile with its trajectory in the plane of the figure, has its highest point at A. The projectile therefore collides (elastically) with the bob of the pendulum at A and makes it move with horizontal speed V₁ as shown. The acceleration due to gravity at the place is g.

(a) If the speed V₁ of the bob of the pendulum is just sufficient to make it travel along the circular path of radius ℓ, derive an expression for the speed V₂ of the bob at the highest point B of the circular path.

(b) Derive an expression for the kinetic energy of the bob in terms of m, ℓ and g just when it starts moving from A.

(c) Obtain an expression for the speed of the bob at C, when the string of the pendulum is horizontal.

(d) What was the kinetic energy of the projectile (sphere S) just before it collided with the bob? Give reason for your answer without writing theoretical steps.

(e) Briefly explain the nature of the motion of the projectile after hitting the bob.

Try to answer the above question which carries 15 points (3+4+4+2+2). I’ll be back with the answer shortly.

AP Physics B and C- Equations to be Remembered in Circular Motion and Rotation

In the section ‘Circular motion and rotation’, the sub sections included as common for AP Physics B and C are

(1) Uniform circular motion and

(2) Torque and rotational statics.

The sub sections included for AP Physics C only are

(1) Rotational kinematics and dynamics and

(2) Angular momentum and its conservation.

Circular motion and rotation’ carries 4% of the total points for AP Physics B and 9% of the total points for AP Physics C.

Here are the important equations you need to remember to tackle the AP Physics B Examination:

(1) When an object is in uniform circular motion, the magnitude of its centripetal acceleration (a_c) is given by

a_c = v²/R where ‘v’ is the speed of the object and R is the radius of the circle. The direction of a_c is always towards the centre of the circle.

The angular speed ω is related to the speed v by

v = ωR.

Therefore, the centripetal acceleration is a_c = ω²R.

If T is the time period of revolution of the object in circular motion and f is its frequency, we have f = 1/T and ω= 2π/T = 2πf.

The centripetal force required to produce circular motion is mv²/R = mω²R

(2) Angular acceleration (α) is the time rate of change of angular velocity and is given by

α = dω/dt

In the case of a body in accelerated rotational motion, the angular velocity (ω) after a time t is given by

ω = ω₀ + αt where ω₀ is the initial angular velocity and and α is the angular acceleration. [This is similar to the equation, v = v₀ + at in linear motion].

The angular displacement (θ) at the instant t is given by

θ = θ₀ + ω₀t + (½) αt² where θ₀ is the initial displacement (at t =0)

[This is similar to the equation x = x₀ + v₀t + (½) at² in linear motion].

(3) Torque (τ) is the moment of force and is the product of force and the lever arm. By lever arm we mean the perpendicular distance (ON in the figure) of the line of action of the force from the origin.

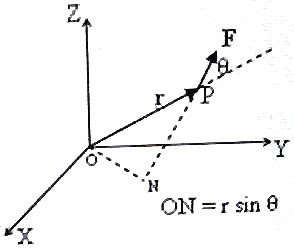
Therefore, Torque τ produced by the force F acting on the particle at P = ON × F.

Since ON = r sinθ where θ is the angle between r and F,

τ = rF sinθ

[Note that torque (τ) is a vector which is the vector product of the position vector r and the force vector F. Therefore, torque τ = r × F]

(4) A rigid body will be in mechanical equilibrium, if the total force and the total torque on the body are zero. The condition of zero net force will ensure that there is no change in the linear momentum and the condition of zero net torque will ensure that there is no change in the angular momentum.

For AP Physics C Examination, you will require the following also (in addition to the above):

(5) Consider a particle of mass m and linear momentum p. If the position vector of the particle is r, the angular momentum L of the particle with respect to the origin is given by

L = r × p

L is a vector whose magnitude is rpsinθ where r is the distance of the particle from the origin, p is the magnitude of the linear momentum vector p and θ is the angle between the vectors r and p.

Angular momentum is the moment of the linear momentum and is the product of linear momentum and the lever arm r sinθ. [By lever arm we mean the perpendicular distance of the line of action of the linear momentum from the origin].

(6) Moment of inertia (I)of a system of particles (as in the case of a rigid body) about an axis (of rotation) is given by

I = ∑mr² where m is the mass of a particle at perpendicular distance r from the axis of rotation and the summation is for all the particles.

Radius of gyration (k) is related to moment of inertia (I) and the mass of the body (M) as

I = Mk²

Note that both I and k depend on the axis of rotation.

Parallel axes theorem states that the moment of inertia (I)of a body about any axis is equal to the sum of the moment of inertia (I_CM )of the body about a parallel axis through its centre of mass and the product Ma² where M is the mass of the body and a is the distance between the two axes:

I = I_CM + Ma²

Perprndicular axes theorem states that the moment of inertia of a lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.

[For example, if the X and Y axes are in the plane of the lamina, the Z-axis is the perpendicular axis and we have I_Z = I_X + I_Y where I_Z, I_X and I_Y are the moments of inertia about the Z, X and Y-axes respectively]

Moments of inertia of some regular bodies are given below:

(i) Thin circular ring (Mass M, Radius R) about its central axis perpendicular to its plane: MR²

A hollow cylinder (pipe) also has the above value for its moment of inertia about its own axis.

(ii) Thin circular ring (Mass M, Radius R) about any diameter: MR²/2

(iii) Thin rod (Mass M, Length L) about a perpendicular axis through the mid point: ML²/12

(iv) Circular disc (Mass M, Radius R) about its central axis perpendicular to its plane: MR²/2

(v) Circular disc (Mass M, Radius R) about its diameter: MR²/4

(vi) Solid cylinder (Mass M, Radius R) about the axis of the cylinder: MR²/2

(vii) Solid sphere (Mass M, Radius R) about its diameter: (2/5)MR²

(viii) Hollow sphere (Mass M, Radius R) about its diameter: (2/3)MR²

(7) Angular momentum (L) is given by

L = Iω where I is the moment of inertial about the axis of rotation and ω is the angular velocity.

This is similar to the expression for linear momentum p = mv. In angular motion (rotational motion) I is to be used in place of m and ω is to be used in place of v.

Newton’s 2^nd law in rotational motion is

τ = dL/dt = d(Iω)/dt

If the moment of inertia (I) is constant, as is the case of a rigid body rotating about a fixed axis, we can write

τ = I (dω/dt) = I α where α is the angular acceleration.

The law of conservation of angular momentum states that in the absence of external torque, the angular momentum of a system remains unchanged. This can be expressed as

I₁ ω₁ = I₂ ω₂ where I₁ and I₂ are the initial and final moments of inertia and ω₁ and ω₂ are the initial and final angular velocities of a system in the absence of external torques.

(8) Acceleration (a) of a body rolling down an inclined plane of inclination θ is given by

a = gsinθ / [1 + (k²/R²)] where R is the radius of the body and k is the radius of gyration about the axis of rolling.

Since Mk² = (2/5)MR² for a solid sphere, k²/R² = 2/5. This is the least value in the case of regular bodies and hence the acceleration a is maximum in the case of a solid sphere. In contrast, in the case of a ring (and pipe), the value of k²/R² is 1 and is the maximum in the case of regular bodies and hence the acceleration a is the minimum in the case of a ring.

If differently shaped bodies are allowed to roll down from the top of an inclined plane, the solid sphere will reach the bottom first and the ring (and the pipe) will arrive last. It is interesting to note that for a given shape, the time of arrival at the bottom is independent of mas and size.

The above equation for acceleration down the plane can also be written as

a = (Mgsinθ) / [M + (I/R²)] where M is the mass of the body; but it will be better to remember the above form in terms of the radius of gyration, k.

(9) Rotational kinetic energy (K) of a body is given by

K = (½) Iω²

(10) A rolling body has translational and rotational kinetic energies. The total kinetic energy of a rolling body is therefore given by

K = (½) Mv² + (½) Iω² where v is the linear velocity of the body

(11) Work (dW) done by a torque τ in producing an angular displacement dθ is given by

dW = τ dθ [By dW we mean the small amount of work done for a small angular displacement dθ]

This is similar to the expression for work, dW = Fds in linear motion.

(12) Power (P) in rotational motion is given by

P = τω

This is similar to the expression for power, P = Fv in linear motion

Different quantities in linear motion and the corresponding quantities in rotational motion (about a fixed axis) are given below:

(a) Displacement x → Angular displacement θ

(b) Velocity v = dx/dt or dr/dt→ Angular velocity ω = dθ/dt

(c) Acceleration a = dv/dt → Angular acceleration α = dω/dt

(d) Mass M→ Moment of inertia I

(e) Linear momentum p = Mv→ Angular momentum L = Iω

(f) Force F = Ma →Torque τ = I α

(g) Work dW = Fds → Work dW = τ dθ

(h) Kinetic energy K = Mv²/2→ Kinetic energy K = Iω²/2

(i) Power P = F v→ Power P = τω

In the next post, we will discus typical questions in this section.

AP Physics B- Answer to Free Response Question on Interference

In the post dated 13^th January 2008, the following free response question for practice was given to you:

Your teacher suggests to you that an interference method could be used to measure the frequency of the sound emitted by two small identical speakers S₁ and S₂ arranged horizontally with a separation of 0.8 m (or any suitable distance) as shown. The speakers are connected in series to a sine wave generator of constant output frequency. Your teacher moves the probe (microphone) of a sound level meter along the horizontal line AB parallel to the line S₁ S₂ and demonstrates to you that at O, equidistant from S₁ and S₂, the intensity of sound is maximum and it varies between maximum and minimum when the probe is moved along OA and OB.

(a) Explain briefly what measurements you will make to enable you to calculate the frequency of the sound emitted by the speakers.

(b) If the distance between the speakers is increased, what quantity you measure is affected and how?

(c) What equations you will use for calculating the frequency? Explain the reason for your answer to (b) based on the relevant equation.

(d) If the distance between the 2^nd maximum on one side of O and the 3^rd maximum on the other side of O is 1.725 m, calculate the frequency of the sound emitted by the speakers, assuming that the speed of sound at the laboratory temperature is 345 ms^–1.

(e) Your teacher asks you to reverse the connection to the terminals of one of the speakers. What change, if any, will this produce in the location of the maxima and minima? Your teacher suggests to you that an interference method could be used to measure the frequency of the sound emitted by two small identical speakers S₁ and S₂ arranged horizontally with a separation of 0.8 m (or any suitable distance) as shown. The speakers are connected in series to a sine wave generator of constant output frequency. Your teacher moves the probe (microphone) of a sound level meter along the horizontal line AB parallel to the line S₁ S₂ and demonstrates to you that at O, equidistant from S₁ and S₂, the intensity of sound is maximum and it varies between maximum and minimum when the probe is moved along OA and OB.

(a) Explain briefly what measurements you will make to enable you to calculate the frequency of the the sound emitted by the speakers.

(b) If the distance between the speakers is increased, what quantity you measure is affected and how?

(c) What equations you will use for calculating the frequency? Explain the reason for your answer to (b) based on the relevant equation.

(d) If the distance between the 2^nd maximum on one side of O and the 3^rd maximum on the other side of O is 1.725 m, calculate the frequency of the sound emitted by the speakers, assuming that the speed of sound at the laboratory temperature is 345 ms^–1.

(e) Your teacher asks you to reverse the connection to the terminals of one of the speakers. What change, if any, will this produce in the location of the maxima and minima? Give reason for your answer.

As promised, I give below the answer:

(a) The mean width (β) of of the interference bands is required and therefore, the distance between the centres of the n^th maxima on either side of the central point O is to be measured. This distance (x_n) will give the width of n bands since the point O is the centre of the zero order maximum. The value of n should be such that the line joining S₁S₂ to the centre of the n^th band is not much different from 90º.

The distance (d) between the speakers (coherent sources) and the distance (D) between the line AB and the line S₁S₂ also are to be measured to facilitate the calculation of the wave length of sound.

(b) If the distance between the speakers is increased, the interference band width is decreased.

(c) The equation for band width is β = λD/d where β is the band width given by β = x_n/n, λ is the wave length of the sound produced by the speakers, D is the distance between the centre of the line S₁S₂ and the point O and d is the separation between the speakers.

From the above equation, λ = βd/D.

The frequency f of the sound can be calculated using the equation

f = v/λ where ‘v’ is the velocity of sound.

Since the fringe width β = λD/d, when the separation between the speakers (d) is increased, β must be decreased as stated in (b).

(d) The distance between the 2^rd maximum on one side of O and the third maximum on the other side of O is 1.725 m. Evidently this is the width of 5 bands since the point O is the centre of the zero order maximum. Therefore,

β = x_n/n = 1.725/5 = 0.345 m so that

λ = βd/D = (0.345×0.8)/6 = 0.046 m and

f = v/λ = 345/0.046 = 7500 Hz.

(e) When the connection to the terminals of one of the speakers is reversed, the phase difference between the sound waves emitted by the speakers becomes 180º. (Earlier, they were in phase and that was why maximum intensity was observed at O). The waves therefore arrive at O with a phase difference of 180º and they interfere destructively, producing minimum intensity at O. Similarly, the intensity will be minimum at all points where it was maximum earlier. In regions where the waves arrived with opposite phase (with phase difference equal to an odd multiple of π) earlier will now become regions of maximum intensity since the waves will reach those regions in phase (with phase difference equal to an even multiple of π). Therefore, the positions of maximum intensity and minimum intensity will get interchanged.